이번 포스팅에서는 데이터 스케일링(Data Scailing)에
대해서 학습하겠습니다.
데이터 스케일링은
데이터 분석 측면에서는
피처 스케일링이라고 한다고 합니다.
피처 = 특성 = 열 = 속성 = 특성 =차원
동일한 말이라고 하고 이 포스팅에서는
'피처'로 이 명칭을 통일해서 설명하겠습니다.
아래 잘 정리된 포스팅을 참고해서
학습해보겠습니다.
[ML] 데이터 스케일링 (Data Scaling) 이란?
스케일링이란? 머신러닝을 위한 데이터셋을 정제할 때, 특성별로 데이터의 스케일이 다르다면 어떤 일이 벌어질까요? 예를 들어, X1은 0 부터 1 사이의 값을 갖고 X2 는 1000000 부터 1000000000000 사이
wooono.tistory.com
1. 데이터 스케일링이란?
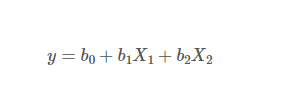
저희가 모델 가중치를 구하는 회귀식이죠.
X1는 0~1사이의 작은값
X2는 1000000~10000000000사이의 X1에 비해 아주 큰 값
y도 1000000~ 100000000사이의 X1에 비해 아주 큰 값을
갖는다고 가정하면
X1의 특성은 y를 예측하는데
큰영향을 주지 않는 걸로 생각할 수 있다고 합니다.
이러한 문제로
데이터 별로 스케일이 다르다면
최적의 가중치가 나오지 않을 뿐더러
X1값이 많이 커지게 되면 메모리에 오버플로우가
발생할 수 있다고 하네요.
즉 스케일링의 타깃은 X(입력값)이 되겠네요.
X의 스케일이 비슷해진다면
모든 데이터가 유사한 영향을 주니깐요.
그래서 스케일링이란! 위의 문제를 해결하기 위해
X(입력값)의 다양한 피처의 스케일의 값을 0~1로
맞춰주는 작업이라고 합니다.
2. 주로 사용되는 스케일링 방식
1) Standardization 표준화
피처들의 평균을 0, 분산을 1로
스케일링 하는 방식이라고 합니다.
음....결국 표준 정규 분포의 속성을 갖도록
피처를 재조정하는 방식입니다.
아래 그림을 보고 이해하자면
여러 범위로 분포된 데이터들을
아래 z의 표준정규분포로서
스케일링 해준다는 뜻 같네요.

이미지 출처 : http://www.ktword.co.kr/test/view/view.php?m_temp1=1995
2) Normalization 정규화
특성들을 특정 범위로 스케일링 하는 것입니다.
주로 0~1 범위을 특정한다고 하네요.
가장 작은 값은 0, 가장 큰 값은 1로
잡고 중간 값들은 비율에 따라서
이 사이의 값을 갖도록
데이터들을 스케일링 하는 방식이라고 하네요.
3. python에서 스케일링 사용하기
앞서 1의 개념을 소개할때
스케일링의 대상은 X(입력값)이라고 했죠?
또 주의사항이 하나 더 있습니다.
우리는 훈련데이터와 평가데이터를 쪼개주는데요,
이 쪼개지는 과정 전에 스케일링을 하게 되면
스케일링 범위의 기준이
두 데이터가 차이가 난다고 합니다.
그렇기 때문에 반드시 데이터를 쪼갠 후에
스케일링을 진행하라고 하네요!
이제 God Scikit - Learn에서 제공하는
4가지의 스케일링을 사용해보겠습니다!
https://scikit-learn.org/stable/modules/classes.html#module-sklearn.preprocessing
API Reference
This is the class and function reference of scikit-learn. Please refer to the full user guide for further details, as the class and function raw specifications may not be enough to give full guidel...
scikit-learn.org
스케일러들은 sklearn.preprocessing이라는 모듈에 있습니다.
이 preprocessiong 안에는
스케일링, 센터링, 정규화, 이진화 방법이 포함된다고 하네요,
1. StandardScaler()
위에서 말한 표준화 방식의 스케일링입니다.
데이터들의 스케일을
표준정규분포 모양으로
스케일링 해줍니다.
최솟값과 최댓값의 크기가 큰
데이터 분석에서
문제가 있을 수 도 있다고 하며,
이상치에 매우 민감하다고 하네요.
회귀보다 분류에 유용하다고 합니다.
sklearn.processing 모듈의 StandardScaler()를 import해주고
각 열의 데이터 크기가 차이나는 행렬을 만들어 주었습니다.
StandardScaler()를 객체화 하고
fit() 함수를 이용해 데이터 형태를 정해주고
transform()함수로 변환해주었습니다.
아래 결과로 엄청 작거나 크게 차이나는 각 컬럼 데이터들도
표준정규분포의
특성에 따라 작은 값으로 스케일링 된 것을
확인할 수 있습니다.
import numpy as np
a = np.array([-192222222222, -1000, -1, 0, 1,10, 100, 1000000, 1000000000]).reshape(-1,1)
#reshape를 해준 이유는 벡터 -> 행렬 변환
from sklearn.preprocessing import StandardScaler
standard_scaler = StandardScaler()
standard_scaler.fit(a)
print(standard_scaler.transform(a))
'''
[[-2.82838951]
[ 0.35147877]
[ 0.35147879]
[ 0.35147879]
[ 0.35147879]
[ 0.35147879]
[ 0.35147879]
[ 0.35149533]
[ 0.36802146]]
'''
2. MinMaxScaler()
각 컬럼 데이터들의
가장 작은값을 0, 가장 큰 값을 1로 기준해서
비율에 따라 0~1값으로
변경해줍니다.
이 방식도 이상치에 매우 민감하다고 합니다.
import numpy as np
a = np.array([-192222222222, -1000, -1, 0, 1,10, 100, 1000000, 1000000000]).reshape(-1,1)
from sklearn.preprocessing import MinMaxScaler
standard_scaler = MinMaxScaler()
standard_scaler.fit(a)
print(standard_scaler.transform(a))
'''
[[0. ]
[0.99482461]
[0.99482461]
[0.99482461]
[0.99482461]
[0.99482461]
[0.99482461]
[0.99482979]
[1. ]]
'''
3. MaxAbsScaler()
각 열의 데이터들을 절대값이 0과 1 사이가
되도록 스케일링합니다.
다시 말하면 모든 값은 -1~ 1사이의 범위를 갖게 됩니다.
역시나 이상치에 매우 민감하다고 합니다.
import numpy as np
a = np.array([-192222222222, -1000, -1, 0, 1,10, 100, 1000000, 1000000000]).reshape(-1,1)
from sklearn.preprocessing import MaxAbsScaler
standard_scaler = MaxAbsScaler()
standard_scaler.fit(a)
print(standard_scaler.transform(a))
'''
[[-1.00000000e+00]
[-5.20231214e-09]
[-5.20231214e-12]
[ 0.00000000e+00]
[ 5.20231214e-12]
[ 5.20231214e-11]
[ 5.20231214e-10]
[ 5.20231214e-06]
[ 5.20231214e-03]]
'''
4.RobustScaler()
평균과 분산이 아닌
중간값과 사분위 값을 사용한다고 합니다.
중간값은 정렬시 중간에 있는 값,
사분위 값은 1/4, 3/4에 위치한 값을 의미한다고 하네요.
(IQR (Interquartile Range) with Box plots 방식
을 채택한다고 하는데 이상치 처리 방식이라고 합니다.)
조금 단순하게 풀어보자면
중앙값의 분포가 아닌
1/4, 3/4에 데이터가 분포된
형태라고 이해됩니다..(맞나요??)
이상치의 영향을 최소화 할 수 있다고 하네요.
import numpy as np
a = np.array([-192222222222, -1000, -1, 0, 1,10, 100, 1000000, 1000000000]).reshape(-1,1)
from sklearn.preprocessing import RobustScaler
standard_scaler = RobustScaler()
standard_scaler.fit(a)
print(standard_scaler.transform(a))
'''
[[-1.90319032e+09]
[-9.91089109e+00]
[-1.98019802e-02]
[-9.90099010e-03]
[ 0.00000000e+00]
[ 8.91089109e-02]
[ 9.80198020e-01]
[ 9.90098020e+03]
[ 9.90099009e+06]]
'''
데이터의 이상치의 비율이나
데이터의 형태에 따라
좋은 스케일링을 선택한다면
머신의 성능을 올릴 수 있다고하니
적극적으로 이용해야 겠습니다.
전체적인 데이터 처리 후 분포도는
아래 링크에서 한번 더 확인하시면 될 것 같습니다!
Compare the effect of different scalers on data with outliers
Feature 0 (median income in a block) and feature 5 (average house occupancy) of the California Housing dataset have very different scales and contain some very large outliers. These two characteris...
scikit-learn.org
'인공지능 개발하기 > Machine Learning' 카테고리의 다른 글
| [Tensorflow] 24. tensorflow GPU 가상환경 설정하기 (0) | 2024.01.20 |
|---|---|
| [Tensorflow] 23. 모델(Model) 구조와 가중치(Weights) 저장하기, 불러오기 (0) | 2024.01.20 |
| [Tensorflow] 21. 범주형 데이터(Categorical Data)를 수치형 데이터(Numeric data)로 변환하기 (0) | 2024.01.20 |
| [Tensorflow] 20. 다중 분류(Multiclass Classification) (0) | 2024.01.13 |
| [Tensorflow] 19. 이진분류(Binary Classification) (0) | 2024.01.13 |


